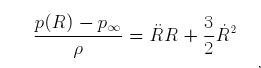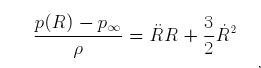b3ta.com board
You are not logged in. Login or Signup
Home » Messageboard » XXX » Message 8380149 (Thread)

# i don't understand
but i'm willing to learn ;)
(I helped save b3ta! Smash Monkey lowering the tone of the whole internet, Sun 18 May 2008, 12:27, archived)
# oh ok
Consider a cavity in a fluid, with a time dependent pressure p(t), the radius R(t) of the bubble is:
(k3b/-\b Peace man., Sun 18 May 2008, 12:32, archived)
# sheirly
that first part of the equation should just be

R-(p&-1) as dividing by P would cancel the others out....however, how can you have infinity in the equation?
(I helped save b3ta! Sir T. Skellington, Sun 18 May 2008, 12:36, archived)
# he's dividing by rho, not p
rho is density, p(R) the pressure at radius R, p(infinity) the asymptotic limit of the pressure as R is tended to infinity
(I helped save b3ta! boris the spider, Sun 18 May 2008, 12:38, archived)
# ahhh i didnt see the rho
and well explained!
(I helped save b3ta! Sir T. Skellington, Sun 18 May 2008, 12:39, archived)
# practice
(I helped save b3ta! boris the spider, Sun 18 May 2008, 12:40, archived)
# stop stealling my thesis
(k3b/-\b Peace man., Sun 18 May 2008, 12:41, archived)
# Science is theft
(I helped save b3ta! boris the spider, Sun 18 May 2008, 12:45, archived)
# Yeah I know I suppose I stole that from Rayleigh and Plesset...
*wistles*
(k3b/-\b Peace man., Sun 18 May 2008, 12:48, archived)
# the thing on the bottom is a rho not a p
and the infinity is a subscript on a p, which is like the pressure at an infinite distance from the bubble (cavity)
(k3b/-\b Peace man., Sun 18 May 2008, 12:39, archived)
# psst
http://www.b3ta.com/board/8380185
(I helped save b3ta! boris the spider, Sun 18 May 2008, 12:41, archived)
# psssst
www.b3ta.com/board/8380197
(k3b/-\b Peace man., Sun 18 May 2008, 12:44, archived)
# I've just had a sudden thought
that looks enormously like the equivalent of the Friedmann equation in a McVittie spacetime. I don't know what I could do with that but it might be worth looking back over an aborted project in the McVittie spacetime.... Hmmmm.


Edit: I probably mean the Raychaudhuri equation rather than the Friedmann equation, since that's the same as the FLRW case.
(I helped save b3ta! boris the spider, Sun 18 May 2008, 12:37, archived)
# you win at science!
(I helped save b3ta! Sir T. Skellington, Sun 18 May 2008, 12:44, archived)
# god no
one tiny little pocket of it. i'm shit at the rest of it.
(I helped save b3ta! boris the spider, Sun 18 May 2008, 12:46, archived)
# I'm finding McVittie space-time hard to digest
*runs back to fluid dynamics*
(k3b/-\b Peace man., Sun 18 May 2008, 12:49, archived)
# That's painful
as is the naked singularity sitting on the event horizon when you try and chew it.
(I helped save b3ta! boris the spider, Sun 18 May 2008, 12:53, archived)
# phwoar naked???
I have a pole now...
(k3b/-\b Peace man., Sun 18 May 2008, 12:57, archived)
# I don't know what it would be like to stick your dick in a black hole
though I can hazard a guess, but I really don't know what it would be like to try and stick your dick through a naked singularity. Either way you probably wouldn't live to tell the tale.
(I helped save b3ta! boris the spider, Sun 18 May 2008, 13:52, archived)